基于 GF-1与Landsat-8的康保县叶面积指数遥感反演研究
(1.林业遥感大数据与生态安全湖南省重点实验室,湖南长沙 410004;2. Department of Geography, Southern Illinois University at Carbon dale,IL 62901 USA)
Modeling LAI of Kangbao county using GF-1 and Landsat-8 image
(1.Key Laboratory of Forestry Remote Sensing Based Big Data & Ecological Security for Hunan Province, Changsha 410004, Hunan, China; 2. Department of Geography, Southern Illinois University at Carbon dale, IL 62901 USA)
LAI; stepwise regression; logistic regression; GWR regression; PCA; GF-1; Landsat-8
DOI: 10.14067/j.cnki.1673-923x.2018.01.008
作者简介:徐晓雨,硕士研究生通信作者:王广兴,教授,博士,博士生导师; E-mail:gxwang@siu.edu
-
以 GF-1和 Landsat8遥感影像为数据源,采用逐步回归、非线性 Logistic回归和基于空间位置的地理加权回归 3种方法,结合 134个野外样地调查数据,在河北省康保县开展叶面积指数反演研究,并对结果进行精度检验。结果 表明:( 1)在荒漠化地区, GF-1和 Landsat-8遥感影像提取的植被指数因子与 LAI均有较高的相关性。运用主成分分析方法对植被指数因子进行处理,可以有效消除各影响因子间的共线性。( 2)基于 GF-1和 Landsat-8影像分别建立的 3种模型,均以地理加权回归决定系数最大,均方根误差最小,反演精度最高。(3)国产 GF-1数据反演 LAI效果优于 Landsat-8,可以代替 Landsat-8数据进行叶面积指数的估测。
Leaf area index (LAI) is an important indicator of forest structural parameter. In this study, a novel method that combined PCA with a linear stepwise regression, a logistic-model and GWR regression was developed to derive an integrated regression model of LAI.A total of 134 sample plots were systematically selected in the study area-Kangbao County, Hebei province and LAI data were collected. Landsat-8 and GF-1 image were acquired. The results were validated using the observations of sample plots and showed that:(1) In the desertification area, the vegetation index and LAI extracted by GF-1 and Landsat-8 had a high correlation. The PCA method can be used to eliminate the collinearity of the vegetation index factors. (2) The estimation accuracy of GWR regression was the highest for both GF-1 and Landsat-8 data with the greatest determination coefficient and smallest root mean square error (RMSE). (3) Inversion of LAI by domestically produced GF-1 data in the study area is better than that of Landsat-8, and can be used as a substitute for Landsat-8 data for estimation of LAI.
引言
叶面积指数被定义为单位地表面积上总绿叶面积的一半 [1]。作为表征植被冠层的主要参数之一 [2],它与植被的蒸腾、光合作用及净初级生产力等生物物理过程密切相关 [3]。现有研究一般集中于农作物、森林叶面积指数和生理生化参数的反演上 [4-8],而对荒漠化地区稀疏植被信息的研究较少。用于反演的数据多以 Landsat、MODIS等国外遥感数据较为常见 [9-13],而对国产遥感数据的应用较少。从现有叶面积指数反演经验模型研究成果来看,植被指数与 LAI之间存在良好的定量关系。模型输入参数少,易于实现,反演效果较好,但影响叶面积指数大小的植被指数因子往往存在相关性,违背了回归分析各因子相互独立的要求。现有研究表明,荒漠化地区叶面积指数大小主要与降水量有关 [14]。降水量是典型的区域变化量,具有一定的空间依赖性,违背了统计学中观测值相互独立的要求。而全域回归模型的回归系数为一个常数,无法反映叶面积指数的局部变化特征及模型参数随研究区空间位置的变化情况 [15]。
主成分分析法( Principal Component Analysis,PCA)通过对建模因子进行最佳综合、简化,将原始变量处理为少数几个主成分,可以克服原始变量因子之间的共线性并保留原始影响因子的主要信息。该方法已成功应用于作物需水量主导因子确定 [16]、土地利用变化遥感监测 [17]、植被信息提取 [18]等研究中。由 Fortheringham提出的地理加权回归 (Geographically Weighted Regression,简称 GWR)模型是对传统全域回归模型的扩展,在多元线性回归模型的基础上引入了空间位置,可以很好地解决模型空间关系的非平稳性。该方法已广泛应用于天然红松分布研究 [19]、城市住宅地价空间结构研究 [20]、森林碳储量空间分布变化 [21]等领域,与传统的全域回归模型相比,取得了较好的效果。基于上述分析,本研究以 GF-1影像为研究对象,与国际普遍认可的 Landsat-8数据进行对比,用主成分分析的方法选取变量,采用逐步回归、非线性 Logistic回归和基于空间位置的地理加权回归 3种方法,在荒漠化地区河北康保县开展叶面积指数反演研究,并对 3种方法所得结果进行对比,一方面得到康保县叶面积指数遥感反演的最佳模型,另一方面探讨国产 GF-1在林业遥感监测中的适用性。
1 研究区与数据收集
1.1 研究区概况
康保县位于河北省西北部张家口市,地理坐标为 114°11′~ 114°56′E, 41°25′~ 42°08′N,总面积 3 365 km2。地势东北高西南低,北部和东部为丘陵区,南部为波状平原区,平均海拔 1 450 m。属温带亚干旱区,雨热同期,年均气温 1.2 ℃,年均降水量 338.5 mm,其中 5—9月降水量为 292.8 mm,占全年降水量的 86%。全县拥有林地 8万 hm2,草场 11万 hm2。近年来,累计完成京津风沙源治理等生态工程 20万 hm2。
1.2 数据准备
1.2.1 样地布设与调查
叶面积指数观测值使用美国 LAI-2000植物冠层分析仪测量,采用系统抽样的方法,在研究区布设 134个样地,抽样间隔为 5 km×5 km,样地大小为 30 m×30 m。在样地对角线及中心点选择 5个 1 m×1 m小样方进行调查(见图1),取 5次测量的 LAI均值作为样地 LAI野外观测值。通过计算残差图分布进行筛选,剔除水体、建筑用地和 2个离群值大的样地数据,实际得到 122个样地数据作为地面观测数据。
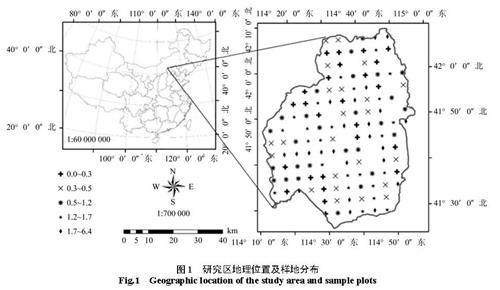
图1 研究区地理位置及样地分布
Fig.1 Geographic location of the study area and sample plots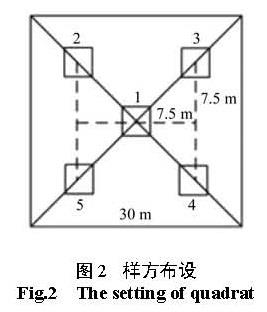
图2 样方布设
Fig.2 The setting of quadrat1.2.2 遥感数据
研究所采用的遥感数据源为 2014年 8月 1日获取的美国陆地卫星 Landsat-8多光谱数据和 2014年 7月 31日获取的同一区域国产 GF-1卫星 WFV数据。在 ENVI5.3软件中,对 Landsat-8数据进行辐射定标和大气校正。为了实现遥感影像空间分辨率与样地大小的近似匹配,按照 4个像元均值计算的方法,将 GF-1影像 16 m空间分辨率上推到 32 m,进行正射校正和大气校正,并以 Landsat-8影像为基准影像进行几何校正。共选择了 25个明显地物点,系统均方根误差为 0.51个像元。
2 研究方法
由于影响 LAI大小的各植被指数因子间具有一定的相关性,难以满足回归分析各因子相互独立的要求,本研究选取主成分分析法对建模因子进行最佳综合、简化,将原始变量线性组合,处理为少数几个彼此互不相关的主成分。该方法不仅可以减少数据处理的工作量,提高效率,同时也克服了各原始变量之间的共线性并保留其主要信息。本研究在 5%水平下根据对叶面积指数影响是否显著来确定叶面积指数的主导影响因子,再采用ArcGIS10.2的空间分析工具进行主成分分析。
地理加权回归考虑局部特征作为权重,以回归的原理研究具有空间或区域分布特征的变量之间的数量关系。它的特点是在线性回归模型中,假定回归系数是观测点地理位置的位置函数,纳入数据的空间特征,可以很好地解决模型的空间非平稳性。模型预测的估计参数和精度强烈依赖于空间权函数和带宽的确定 [22]。GWR模型表示如下:
yi =β0(ui,vi)+β1(ui,vi)x1i+β2(ui,vi)x2i+…+βn(ui,vii)xni+ε。(1)
式中: (ui,vi)表示样地点的坐标; yi表示 i点处的因变量,本研究中表示 i点处的 LAI值;n表示变量的数目; x1i~ xni表示第 n个变量在点的值; β0表示截距; β0~ βn表示第 n个变量的估计参数; ε是误差项。
对野外实际调查数据筛选后得到的 122个样地数据,选取 2/3的样地作为建模样本, 1/3的样地作为检验样本(含 40个样地)。选用决定系数(R2)和均方根误差( RMSE)对模型进行精度评价。R2反映了估测值与实际值之间的拟合程度,其值越接近 1,说明对应的估测模型可靠性越高。 RMSE反映了估测值与实际值的偏差,其值越小模型精度越高。
3 结果与分析
3.1 逐步回归分析
研究选取的变量因子,除了Landsat-8 和GF-1的原始波段及波段倒数外,还考虑了各种植被指数因子,包括归一化植被指数 NDVI、差值植被指数 DVI、土壤调节植被指数 SAVI、比值植被指数 SR、增强型植被指数 EVI、大气抗阻植被指数 ARVI。计算叶面积指数与光谱变量之间的 Pearson相关系数,在 0.05水平下,对于 Landsat-8相关性最高的因子为 NDVI(0.671),对于 GF-1,相关性最高的因子为 SAVI025(0.682)。用 SPSS22.0软件进行逐步回归分析,结果如表1所示。
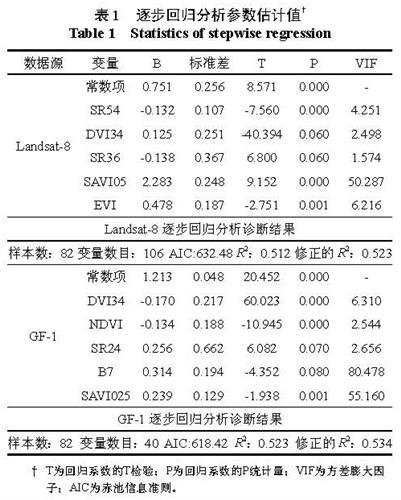
表1 逐步回归分析参数估计值†
表1说明,尽管 R2和修正的 R2都比较高,但在 Landsat-8逐步回归模型中,SAVI05的 VIF值大于10,在GF-1 逐步回归模型中,B7 和SAVI025均大于10。说明直接以光谱因子作为自变量建立逐步回归模型时,回归方程变量冗余,自变量之间存在共线性,不能满足变量相对独立的假定前提。
Table 1 Statistics of stepwise regression为了消除各光谱因子间的共线性,对Landsat-8和GF-1 获得的光谱因子进行主成分分析,均保留前5 个主成分,使其累计贡献率大于85%,以前5 个主成分作为新的变量因子来参与建模,结果见表2。
表2说明,对原始光谱因子进行主成分分析后,全部变量的VIF 值都小于10,共线性问题得到解决。同时,AIC 值降低,R2、修正的R2 增加,说明经过对光谱因子的主成分分析,回归效果得到一定改善。
3.2 Logistic 回归分析
以PCA 方法筛选出的前5 个主成分作为Logistic 回归模型的建模因子,对数据进行归一化处理,利用R 统计软件建立Logistic 回归模型,公式如下。
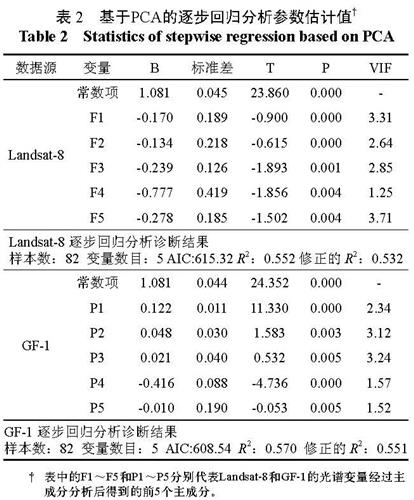
表2 基于PCA的逐步回归分析参数估计值†
Table 2 Statistics of stepwise regression based on PCA
式中: 表示LAI;F1 ~ F5 和P1 ~ P5 分别代表Landsat-8 和GF-1 的光谱变量经过主成分分析后得到的前5 个主成分。
3.3 地理加权回归分析
利用ArcGIS10.3 软件空间统计模块进行空间自相关检验。LAI 的空间自相关系数Moran I 为0.145,Z 为2.204,P 为0.027,存在着较强的空间自相关性。
以LAI 作为因变量,5 个主成分作为自变量,用GWR4.0 软件进行地理加权回归分析。空间权函数设置为Gaussian 函数,核函数选用Adaptivebi-square,带宽经AICc 方法多次验证,Landsat-8确定为21 678 m,GF-1 确定为26 019 m。在ArcGIS10.3 中提取遥感影像每个像元的坐标,用5 个主成分因子的灰度图提取出每个像元的值,导入GWR4.0,得到每个像元对应的自变量系数值,结果如表3 所示。
对比表2 和表3 可知,逐步回归各个变量的系数都落在GWR 模型对应的变量系数取值范围内。各变量系数Q1 与Q3 的间距均小于逐步回归变量系数的一倍标准差间距。说明针对本研究区,
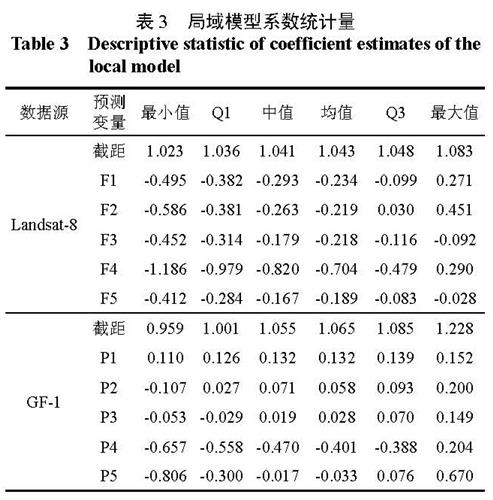
表3 局域模型系数统计量
Table 3 Descriptive statistic of coefficient estimates of the local modelGWR 模型参数存在一定的空间非平稳性,相对于逐步回归分析能反映更多的空间变异信息。
3.4 模型精度验证
对GF-1 和Landsat-8 分别进行模型的精度验证,分别计算决定系数R2 和均方根误差RMSE,结果如表4 所示。
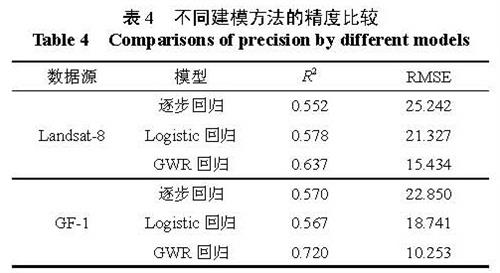
表4 不同建模方法的精度比较
Table 4 Comparisons of precision by different models表4说明,基于GF-1 和Landsat-8 分别建立的3 种模型中,均以GWR 模型决定系数R2 最大,均方根误差最小,反演精度最高;Logistic 回归模型次之,逐步回归模型精度较低。同时对比GF-1和Landsat-8 影像反演结果,基于GF-1 影像建立的3 种模型的精度均略大于Landsat-8 影像的反演精度,表明GF-1 影像反演叶面积指数的效果要优于Landsat-8 影像。
3.5 康保县叶面积指数空间分布
以反演精度最高的GWR 模型为例估计康保县叶面积指数及其分布,结合主成分因子灰度图和GWR 模型对应的系数矩阵,计算每个像元的叶面积指数值,生成叶面积指数分布图。图3(a)、(b)分别为基于Landsat-8 和 GF-1 GWR 回归模型的康保县叶面积指数空间分布。
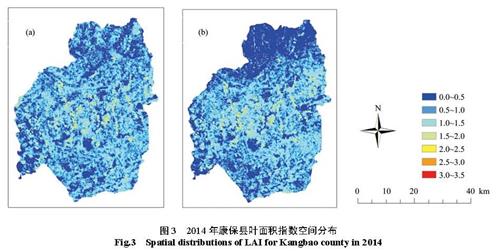
图3 2014 年康保县叶面积指数空间分布
从图3 中可以看出,Landsat-8 和GF-1 遥感数据建立的GWR 模型预测结果所反映的康保县叶面积指数空间分布趋势基本一致,植被覆盖度高的地方,叶面积指数越大;中叶面积指数区域主要零星分布在康保县中部,低叶面积指数区域主要分布在北部,少量分布在南部;模型预测的叶面积指数值大小和分层分布存在差异,其中GF-1 的GWR 模型不同等级的叶面积指数值分层更明显。
Fig.3 Spatial distributions of LAI for Kangbao county in 2014
4 结论与讨论
4.1 结 论
研究以Landsat-8 和GF-1 影像为数据源,采用逐步回归、Logistic 回归和GWR 方法,结合地面调查数据,开展康保县叶面积指数遥感反演研究。首先分析影像各波段反射率,计算植被指数及其衍生指数,用主成分分析方法消除各植被指数之间的共线性,保留累计贡献率大于85% 的前5 个因子,运用逐步回归、Logistic 回归和GWR方法开展叶面积指数模拟,对模拟结果进行精度验证,得到以下结论:
(1)在荒漠化地区,基于GF-1 和Landsat-8提取的植被指数与叶面积指数均有较高的相关性。使用植被指数法估测叶面积指数时两种数据均表现良好,一方面是因为它们都具有较高分辨率;另一方面,荒漠化地区植被类型大多为稀疏草地,植被指数没有达到饱和。应用主成分分析法对光谱变量进行处理,可以有效消除其共线性。
(2)Logistic 回归模型在预测植被区叶面积指数时效果较好,但在非植被区出现了过低估计的现象。对于两种数据,均以GWR 回归效果最好,能准确地反映叶面积指数随空间位置的变化情况,对区域叶面积指数的估算具有一定的借鉴意义。与线性模型相比,非线性模型更适合叶面积指数的反演。
(3)GF-1数据估测叶面积指数的精度要略高于 Landsat-8数据,可以代替 Landsat-8数据用于叶面积指数的估测,而且,其空间分辨率更高,重访周期更短,覆盖面积也更大。
4.2 讨论
与同类研究相比,基于 GWR的叶面积指数反演方法是有效的,其估计结果精度高于传统回归方法。现有研究中,基于 GWR模型的扩展模型还包括半参数地理加权回归模型、地理加权 Logistic回归模型等。这些模型是否适用于叶面积指数反演,是否能得到更好的反演结果,都值得进一步研究。
此次研究样地设计采用系统抽样的方式,样地类型没有完全覆盖所有地类,反演误差主要在非林地区域。因此,下一步应采用分层抽样的方式来布设样地,开展叶面积指数反演,以进一步减小误差。
-
参考文献
- [1] CHEN J M, BLACK T A. Defining leaf area index for non‐flat leaves [J]. Plant, Cell & Environment, 1992, 15(4):421-429.
- [2] Huang M, Jinjun J I. The spatial-temporal distribution of leaf area index in China: a comparison between ecosystem modeling and remote sensing reversion [J]. Acta Ecologica Sinica, 2010, 30(11):3057-3064.
- [3] Yan H, Wang S Q, Billesbach D, et al. Global estimation of evapotranspiration using a leaf area index-based surface energy and water balance model[J]. Remote Sensing of Environment, 2012, 124(9):581-595.
- [4] 任建强 ,陈仲新 ,周清波 ,等 .基于叶面积指数反演的区域冬小麦单产遥感估测 [J].应用生态学报 , 2010, 21(11):2883-2888.
- [5] Grace J, Gash J. Carbon dioxide uptake by an undisturbed tropical rain forest in southwest Amazonia, 1992 to 1993[J]. Science, 1995, 270(5237):778-780.
- [6] 孙华 ,罗朝沁 ,林辉 ,等 .基于 k-NN算法的叶面积指数遥感反演 [J].中南林业科技大学学报 ,2016,36(12):11-17.
- [7] 凌成星 ,鞠洪波 ,张怀清 ,等 . 基于植被指数比较的湿地区域 LAI遥感估算研究 [J]. 中南林业科技大学学报 ,2016, 36(5):11-18.
- [8] 孙华 ,鞠洪波 ,张怀清 ,等 .偏最小二乘回归在 Hyperion影像叶面积指数反演中的应用 [J].中国农学通报 , 2012, 28(7): 44-52.
- [9] 刘洋 ,刘荣高 ,刘纪远 ,等 .基于 MODIS数据反演作物叶面积指数 [C]// 2008海峡两岸遥感大会 . 2008.
- [10] 韩桂华 ,王强 ,刘丹丹 .基于多角度遥感物理模型的叶面积指数反演 [J].测绘科学 , 2010, 35(3):77-79.
- [11] 刘振波 ,刘杰 .森林冠层叶面积指数遥感反演——以小兴安岭五营林区为例 [J].生态学杂志 , 2015, 34(7):1930-1936.
- [12] 杨敏 ,林杰 ,顾哲衍 ,等 .基于 Landsat 8 OLI多光谱影像数据和 BP神经网络的叶面积指数反演 [J]. 中国水土保持科学 , 2015, 13(4):86-93.
- [13] 谷成燕 ,杜华强 ,周国模 ,等 .基于 PROSAIL辐射传输模型的毛竹林叶面积指数遥感反演 [J]. 应用生态学报 , 2013, 24(8):2248-2256.
- [14] 胡琦 .内蒙古地区多时间尺度气候变化及草地叶面积动态响应研究 [D].北京 :中国农业大学 ,2016.
- [15] 覃文忠 .地理加权回归基本理论与应用研究 [D].上海 :同济大学 , 2007.
- [16] 王景雷 ,康绍忠 ,孙景生 ,等 .基于 PCA和 GWR的作物需水量空间分布估算 [J]. 科学通报 ,2013(12):1131-1139.
- [17] 黎夏 ,叶嘉安 .利用主成分分析改善土地利用变化的遥感监测精度——以珠江三角洲城市用地扩张为例 [J].遥感学报 , 1997(4):282-289.
- [18] 刘瑜 ,韩震 ,李睿 .基于主成分分析和植被指数的潮滩植被信息提取研究 [J]. 遥感信息 ,2010(4):45-50.
- [19] 王烁 ,李凤日 ,赵颖慧 ,等 . 基于空间模型的白河林业局天然红松分布 [J]. 北京林业大学学报 ,2015,37(10):73-85.
- [20] 张洁 . 基于 GWR模型的城市住宅地价空间分异研究 [D].杭州 :浙江大学 ,2012.
- [21] 刘畅 ,李凤日 ,贾炜玮 ,等 . 基于局域统计量的黑龙江省多尺度森林碳储量空间分布变化 [J]. 应用生态学报 , 2014, 25(9): 2493-2500.
- [22] Fotheringham A S, Brunsdon C, Charlton M. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships[M]. Geographical analysis, 2003, 35(3): 272-275.
- [1] CHEN J M, BLACK T A. Defining leaf area index for non‐flat leaves [J]. Plant, Cell & Environment, 1992, 15(4):421-429.
中南林业科技大学学报
